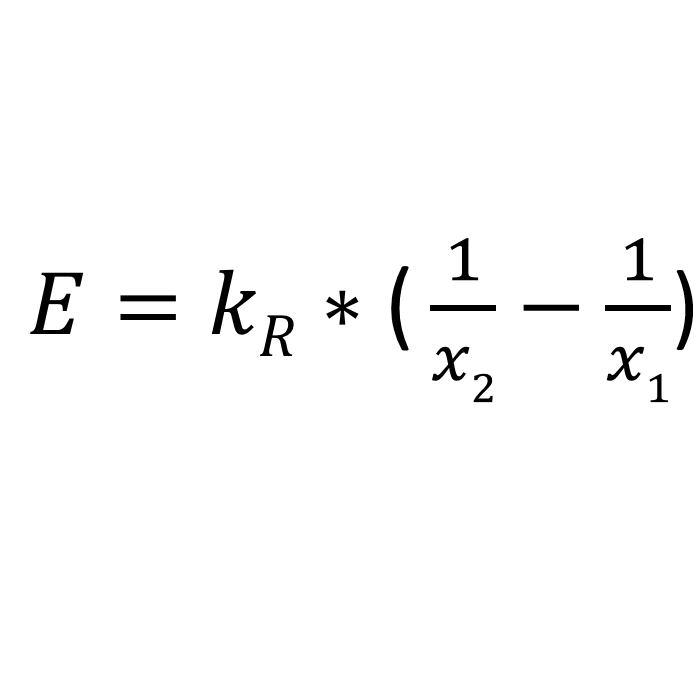
Dimensionsanalysis

Dimensional analysis helps to develop calculation formulae on the basis of experiments.

Dimensional analysis is a method by which physical quantities are traced back to their base units (e.g. length, time, mass) and converted into unit-consistent equations - usually based on the International System of Units (SI). In experimental process engineering, it is often used to convert empirically observed phenomena into formulae that remain valid regardless of the system of units used.

Such equations enable a quantitative description of process engineering effects, e.g. during comminution, grinding, agglomeration or dispersion. Even if they appear formally physically correct, they are essentially based on observed relationships. The underlying physical laws have not yet been discovered. They are therefore referred to as dimensionally consistent approximations.

In practice, dimensional analysis is a valuable tool for modelling, scaling and transferring results from pilot plant tests to industrial processes.

One example is the Rittinger law. This equation is based on the assumption that the energy required for comminution is proportional to the newly generated surface area, which applies relatively well to fine comminution.

• E: Specific energy requirement (e.g. kJ/kg)
• x1: Initial grain diameter (m)
• x2: End grain diameter (m)
• kR: Rittinger constant; material-dependent in the dimension: [m³/s²])