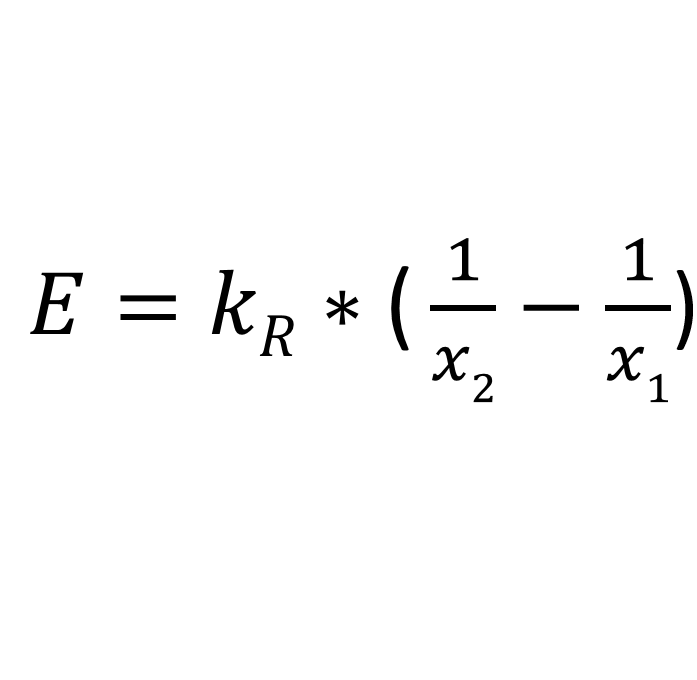
Analisi delle dimensioni
L'analisi dimensionale aiuta a sviluppare formule di calcolo sulla base di esperimenti.
L'analisi dimensionale è un metodo che consente di ricondurre le grandezze fisiche alle loro unità di base (ad esempio, lunghezza, tempo, massa) e di convertirle in equazioni coerenti con le unità di misura, solitamente basate sul Sistema Internazionale di Unità di Misura (SI). Nell'ingegneria dei processi sperimentali, viene spesso utilizzata per convertire i fenomeni osservati empiricamente in formule che rimangono valide indipendentemente dal sistema di unità di misura utilizzato.
Tali equazioni consentono di descrivere quantitativamente gli effetti dell'ingegneria di processo, ad esempio durante la comminuzione, la macinazione, l'agglomerazione o la dispersione. Anche se appaiono formalmente corrette dal punto di vista fisico, si basano essenzialmente su relazioni osservate. Le leggi fisiche sottostanti non sono ancora state scoperte. Si parla quindi di approssimazioni dimensionalmente coerenti.
In pratica, l'analisi dimensionale è uno strumento prezioso per modellare, scalare e trasferire i risultati dei test degli impianti pilota ai processi industriali.
Un esempio è la legge di Rittinger. Questa equazione si basa sul presupposto che l'energia necessaria per la sminuzzatura sia proporzionale alla nuova superficie generata, il che si applica relativamente bene alla sminuzzatura fine.
- E: fabbisogno energetico specifico (ad es. kJ/kg)
- x1: diametro iniziale del grano (m)
- x2: Diametro del grano finale (m)
- kR: costante di Rittinger; dipendente dal materiale nella dimensione: [m³/s²])
