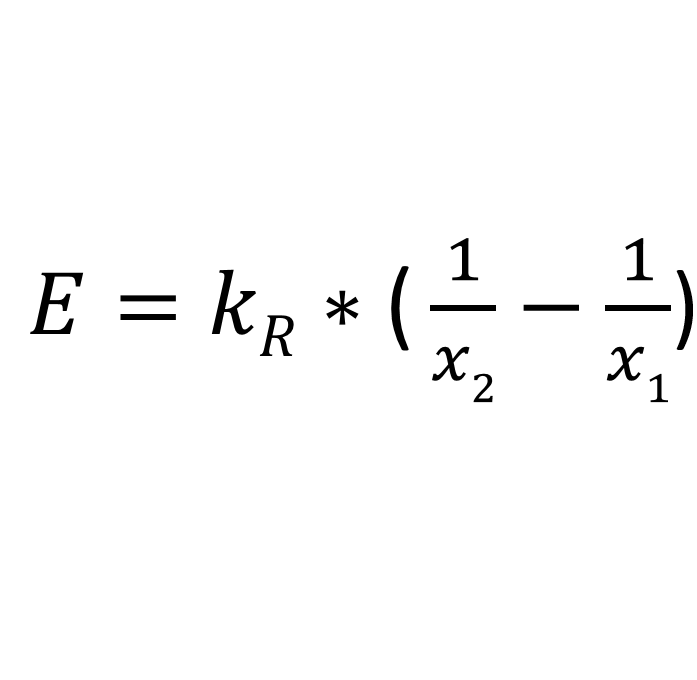
Dimensionsanalyse
Die Dimensionsanalyse hilft bei der Entwicklung von Berechnungsformeln auf der Grundlage von Experimenten.
Die Dimensionsanalyse ist eine Methode, mit der physikalische Größen auf ihre Basiseinheiten (z. B. Länge, Zeit, Masse) zurückgeführt und in einheitenkonsistente Gleichungen - in der Regel auf der Basis des Internationalen Einheitensystems (SI) - überführt werden. In der experimentellen Verfahrenstechnik dient sie häufig dazu, empirisch beobachtete Phänomene in Formeln zu überführen, die unabhängig vom verwendeten Einheitensystem gültig bleiben.
Solche Gleichungen ermöglichen eine quantitative Beschreibung verfahrenstechnischer Effekte, z. B. beim Zerkleinern, Mahlen, Agglomerieren oder Dispergieren. Auch wenn sie formal physikalisch korrekt erscheinen, beruhen sie im Wesentlichen auf beobachteten Zusammenhängen. Die zugrunde liegenden physikalischen Gesetzmäßigkeiten sind noch nicht entdeckt. Man spricht daher von dimensionsanalytisch konsistenten Näherungen.
In der Praxis ist die Dimensionsanalyse ein wertvolles Werkzeug für die Modellbildung, die Skalierung und die Übertragung von Ergebnissen aus Technikumsversuchen auf industrielle Prozesse.
Ein Beispiel ist das Rittinger-Gesetz. Dieser Gleichung liegt die Annahme zugrunde, dass die zur Zerkleinerung erforderliche Energie proportional zur neu erzeugten Oberfläche ist, was für die Feinzerkleinerung relativ gut zutrifft.
- E: Spezifischer Energiebedarf (z.B. kJ/kg)
- x1: Anfangskorndurchmesser (m)
- x2: Endkorndurchmesser (m)
- kR: Rittinger-Konstante; materialabhängig in der Dimension: [m³/s²])
